Writing Pendulum Assembly — or — Crafting Code For The Clockwork Virtual Machine
Pendulum is the virtual machine at the heart of Clockwork 3.x, and provides the flexibility for both configuration management applications (i.e. Clockwork proper) and distributed remote execution and data gathering (Clockwork's exciting new Mesh framework).
For the record, if you want to use Clockwork (and who wouldn't?) you don't have to write any code; Clockwork helpfully translates your policy manifests into Pendulum assembly for you. And if you want to use Mesh, you still don't have to get your hands dirty with code.
No, this post is for the indomitable hacker who likes to get her hands into a thing, up to the elbows if necessary, and figure out how it works.
Hello, World!
Let's just get this one out of the way.
fn main
print "Hello, World!\n"
fn and print are opcodes, short for operation code. Each opcode
instructs the Pendulum VM to perform some computation, and can take up to
two arguments. Here, fn is followed by a label ("main"), and defines the
start of a function. Since Pendulum is styled after low-level assembly
languages, it lacks block structure and can only support functions by
associating function names with their code entry points.
The print opcodes does just what you think it does; prints its string
argument to standard output.
If you've got a build of Clockwork handy, you can use the included pn
utility to compile and run the example:
$ cat hello.pn
fn main
print "Hello, World!\n"
$ ./pn -S hello.pn
$ ./pn hello.pn.S
Hello, World!
Check the man page for pn(1) for more information.
Register Machines
The Pendulum VM is a register machine, not a stack machine. It consists of a set of 16 general-purpose registers, %a - %p, an instruction pointer, and an accumulator.
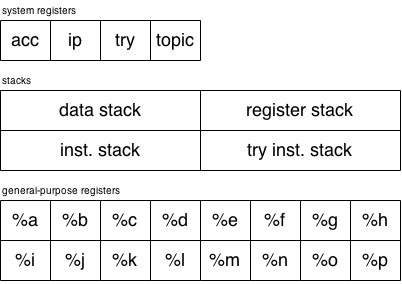
The set opcode stores a value into one of the general-purpose registers:
fn main
set %a "Hello, World!\n"
print %a
The print opcode has a trick up its sleeve. If you give it a format
string, it can pull information out of the general-purpose registers, format
them and print the result.
fn main
set %a "World"
print "Hello, %[a]s\n"
A format specifier is just the name of a register, inside of '%[...]',
followed by a printf-format specifier. Really, the '[...]' is interposed
between the '%' and the rest of the specifier. See printf(3) for details.
Some Basic Opcodes
The basic arithmetic operators are add, sub, mult, and div. They
each take two arguments, a register and a value. The register holds one of
the operands (the leftmost one).
set %a 42
add %a 8 ;; %a == 50
sub %a 17 ;; %a == 33
mult %a 2 ;; %a == 66
div %a 3 ;; %a == 22
The mod opcode provides arithemtic modulo, the remainder after division.
It also takes two arguments, a register and a value:
set %a 9
mod %a 8 ;; %a == 1
Pendulum has several comparison opcodes. eq, lt, lte, gt, and gte
provide numeric comparison, while streq compares character strings for
equality. Each of these opcodes takes two arguments, compares them to one
another, and stores the result as an integer in the accumulator.
The acc opcode copies the value in the otherwise inaccessible accumulator
into a named register:
eq 42 42
acc %a
print "42 == 42 ? acc = %[a]i\n"
Finally, we have the jump opcodes, jmp, jz, and jnz. These directly
manipulate the instruction pointer register. All of these take relative
offsets (like +1 or -3), which define a number of opcodes to skip over.
You can also define labels and jump to them, by name.
It is illegal to jump across function boundaries. Luckily, labels with the same names, in different functions, are distinct.
jmp is an unconditional jump. It works like goto:
fn main
print "Pendulum is "
jmp +1
print "not " ; never executed
print "very cool\n"
will print Pendulum is very cool\n
jz (jump if zero) checks the accumulator and changes the
instruction pointer if the accumulator is 0. On the contrary, jnz
(jump if not zero) only jumps when the accumulator is
any other value. If the conditionas are not met, instructions
continues with the next op.
Obviously, this lets us implement if / else conditionals:
;;
;; is %a an even number?
;;
fn even?
mod %a 2
eq 0
jz +2
print "%[a]i is even\n" ;; if (a % 2 == 0)
retv 0
print "%[a]i is odd\n" ;; else
retv 1
They also let us implement loops:
;;
;; countdown from %a to 0
;;
fn countdown
again:
eq %a 0
jz boom
print "%[a]i...\n"
sub %a 1
goto again
boom:
print "BOOM!\n"
Pendulum isn't all that picky about whitespace between statements.
Sometimes you'll see a conditional and a jump on the same, line. Usually
(although not always) the jump is a jz:
fn test
eq %a 42 jz +1
ret
print "a is not 42\n"
That's idiomatic Pendulum for if a == 42.
Meet My Friend, Fibonacci
We've now got enough Pendulum Assembly under our belts to write the next most obligatory learning-a-new-language example: calculating Fibonacci numbers!
To recap, for the mathematically discinclined, the Fibonacci sequence is:
$$(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 38, 144, 233, 377, …)$$
Each Fibonacci number if the sum of the preceeding two Fibonacci numbers, or,
$$F_n = F_{n-1} + F_{n-2}$$
;;
;; Calculate the nth Fibonacci number
;;
fn fibonacci
gte %n 2 jz +1 ;; F(0) = 1
retv 1 ;; F(1) = 1
sub %n 1 ;; first we calculate n - 1
call fibonacci ;; then F(n - 1)
acc %o ;; storing the value in %o
sub %n 1 ;; then, calculate n - 2
call fibonacci ;; and F(n - 2)
acc %p ;; storing the value in %p
add %o %p ;; add the two values...
retv %o ;; and return the sum
And here's a looping main function that calcualtes the first 14 Fibonacci numbers (any more and we run into stack problems because of the recursion)
fn main
set %n 0
again:
gte %n 14 ;; loop termination; after
ret ;; 14 numbers, we're done.
call fibonacci ;; calculate F(%n)
acc %a ;; store it in %a, temporarily
print "F(%[n]i) = %[a]i\n" ;; and then print
add %n 1 ;; increment %n and
jmp again ;; do it again
And here's the output!
F(0) = 1
F(1) = 1
F(2) = 2
F(3) = 3
F(4) = 5
F(5) = 8
F(6) = 13
F(7) = 21
F(8) = 34
F(9) = 55
F(10) = 89
F(11) = 144
F(12) = 233
F(13) = 377
Looks correct!
To get around the recursion stack overflow problem (try to calculate F(16) and you'll see what I mean), you could find a recurrence relation for Fibonacci numbers. If that type of stuff interests you, I highly recommend Knuth's Concrete Mathematics textbook (most likely available at your local library).
Closing Arguments
Pendulum is a complete and simple assembly language. The opcodes are straightforward and while the official documentation is still mostly non-existent, you can look through the opcodes.yml file, and src/vm.c on github for more information.
Hopefully in the coming weeks I'll find time to cover the fs.* opcodes,
the authentication database and user/group management.
Code Examples
Here's the code from this article, available for download:
